KamiertopのBlogSite
KamiertopのBlogSite

3D Gaussian Splatting for Real-Time Radiance Field Rendering

用于实时辐射场渲染的三维高斯泼溅

kamiertop kamiertop 收录于 Paper
 约 3900 字 预计阅读 8 分钟 
/paper/3dgs/contrast.jpg
Project_Page https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/ card image

研究背景

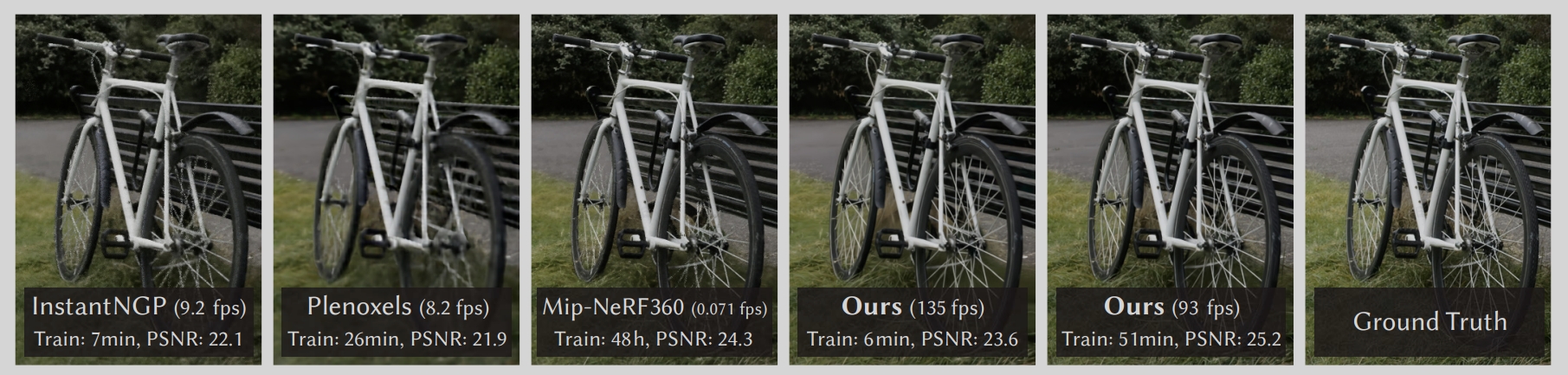
Neural Radiance Field（NeRF）技术在多视角图像合成领域取得显著进展，现有方法在训练和渲染速度上存在瓶颈，无法实现实时高质量渲染
提出一种基于3D高斯分布的场景表示方法，经过优化、密度控制、Tile-Based 光栅化实现快速训练，实时渲染

关键贡献

  1. 3D高斯分布表示
  2. 优化与密度控制
  3. 基于瓦片的GPU高速渲染

方法总览

方法总览

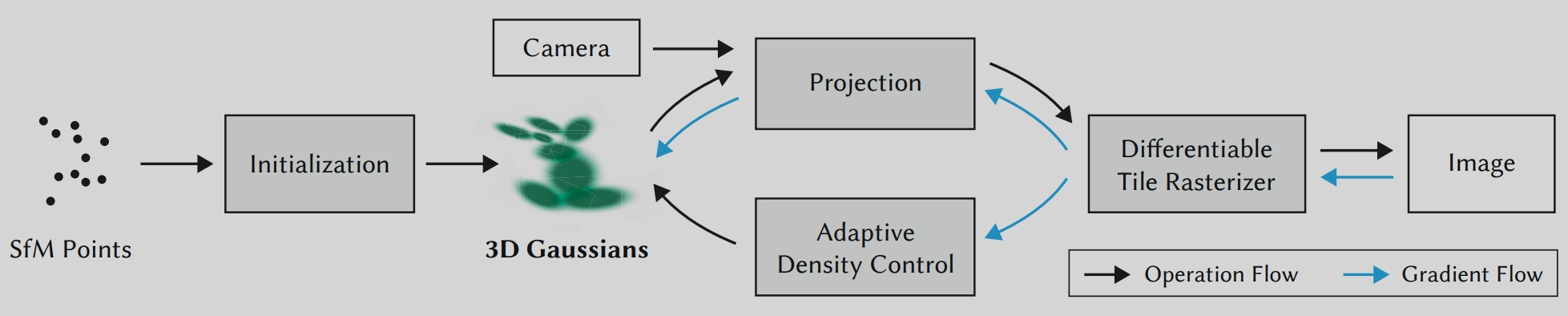
  1. 使用SFM算法从静态场景的多视角图像得到稀疏点云

  2. 以稀疏点云为基础，为每个点创建3D高斯，定义核心属性

    1. 位置（均值μ）：使用SFM点坐标
    2. 协方差矩阵（Σ）：初始设为各向同性（轴长=到最近3个点的平均距离）
    3. 不透明度（α）：初始值通过梯度友好的SIGMOID函数约束在[0,1)
    4. 颜色标识：采用球谐函数（SH)编码，初始仅优化0阶分量

  3. 给定一个相机视角：将3DGS投影到2D图像空间

  4. 使用瓦片式可微光栅化器，基于当前的3D高斯集合渲染出该相机视角下的场景图像

  5. 对比“渲染图”与“该视角下的真实图”，使用损失函数计算误差

  6. 反向传播更新3DGS的关键参数

  7. 自适应密度控制

技术细节

3DGS的数学表示

G(x)=e−12(x)TΣ−1(x) G(x)=e^{-\frac{1}{2}(x)^{T}\Sigma^{-1}(x)}

协方差矩阵的分解优化

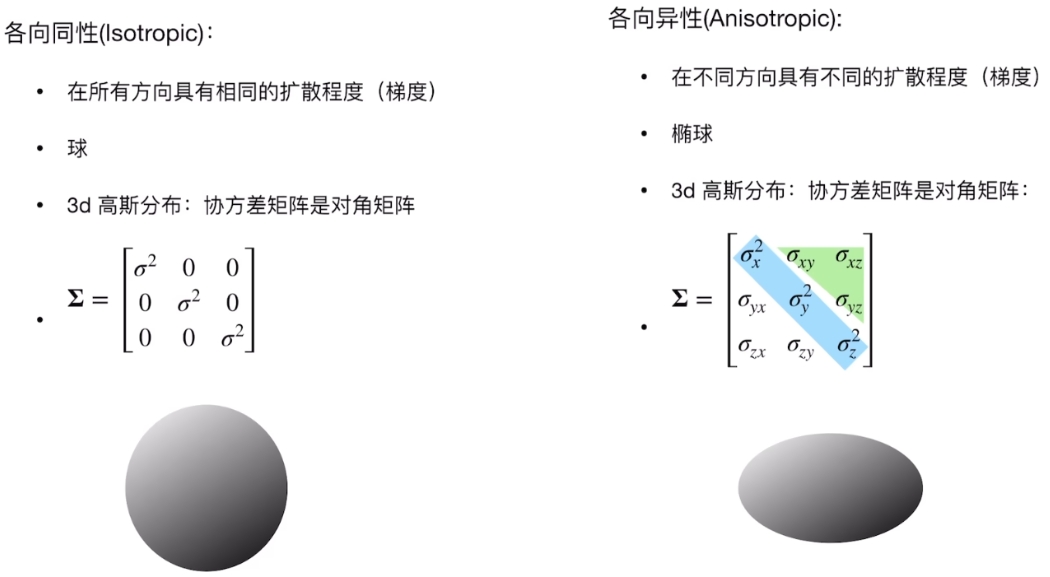
各向同性和各向异性

从仿射变换理解高斯分布

任意3D高斯可以看作标准高斯通过仿射变换得到的：

标准高斯（球形，各向同性）：

G0(x)=exp⁡(−12xTΣ0x)G_0(\mathbf{x}) = \exp\left(-\frac{1}{2}\mathbf{x}^T \Sigma_0 \mathbf{x}\right)

协方差矩阵为单位矩阵 Σ0=I\Sigma_0 = I，在3D空间中是一个标准球体。

仿射变换将标准球体变换为任意椭球：

y=Ax+μ\mathbf{y} = \mathbf{A}\mathbf{x} + \mu

其中：

  • A\mathbf{A}：线性变换矩阵（拉伸+旋转）
  • μ\mu：平移向量（高斯中心位置）

变换后的协方差矩阵变为：

Σ=AIAT\Sigma = \mathbf{A} \mathbf{I} \mathbf{A}^T

分解为旋转和缩放

将线性变换矩阵 A\mathbf{A} 分解为缩放和旋转的组合：

A=RS\mathbf{A} = \mathbf{R}\mathbf{S}

其中：

  • S：缩放矩阵，S=diag(sx,sy,sz)\mathbf{S} = \text{diag}(s_x, s_y, s_z)，将球体沿三个轴拉伸
  • R：旋转矩阵，R∈SO(3)\mathbf{R} \in SO(3)，改变椭球的朝向

代入协方差矩阵公式：

Σ=AAT=(RS)(RS)T=RSSTRT\Sigma = \mathbf{A}\mathbf{A}^T = (\mathbf{R}\mathbf{S})(\mathbf{R}\mathbf{S})^T = \mathbf{R}\mathbf{S}\mathbf{S}^T\mathbf{R}^T

特征值分解角度

Σ=QΛQT=QΛ1/2Λ1/2QT=(QΛ1/2)(QΛ1/2)T \begin{align} \Sigma &= Q \Lambda Q^T \\ &= Q \Lambda^{1/2} \Lambda^{1/2} Q^T \\ &= (Q \Lambda^{1/2}) (Q \Lambda^{1/2})^T \end{align}

优化参数

协方差矩阵必须保持正半定性（所有特征值≥0），直接优化9个元素可能导致无效矩阵。

使用分解形式 Σ=RSSTRT\Sigma = \mathbf{R}\mathbf{S}\mathbf{S}^T\mathbf{R}^T 的优势：

  • 只需优化7个参数（四元数[w，x,y,z]+3个缩放参数[x,y,z]）
  • 天然保证 Σ 正半定
  • 梯度下降不会产生无效矩阵

高斯分布的2D投影

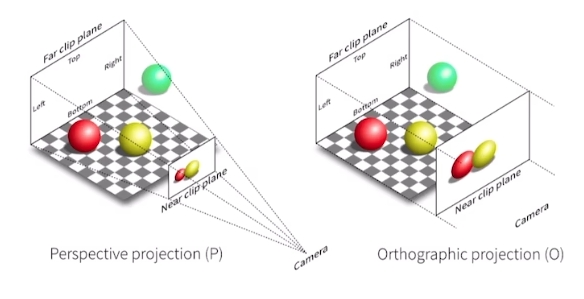
projection

给定一个视角变换矩阵 W（世界坐标→相机坐标），3D高斯投影到2D图像平面的协方差矩阵为：

Σ′=JWΣWTJT\Sigma' = J W \Sigma W^T J^T

其中：

  • W：视图变换矩阵（旋转+平移）
  • J：雅可比矩阵（对线性变换的局部线性近似）
  • Σ’：投影后的2D协方差矩阵（2×2）

投影过程：

  1. 3D高斯中心 μ 投影到屏幕坐标 μ'
  2. 3D椭球通过仿射近似变换为2D椭圆
  3. 得到2D高斯参数（μ’, Σ’），用于后续渲染

关键：投影保持了高斯的可微性，允许梯度反传到3D参数

球谐函数表示颜色

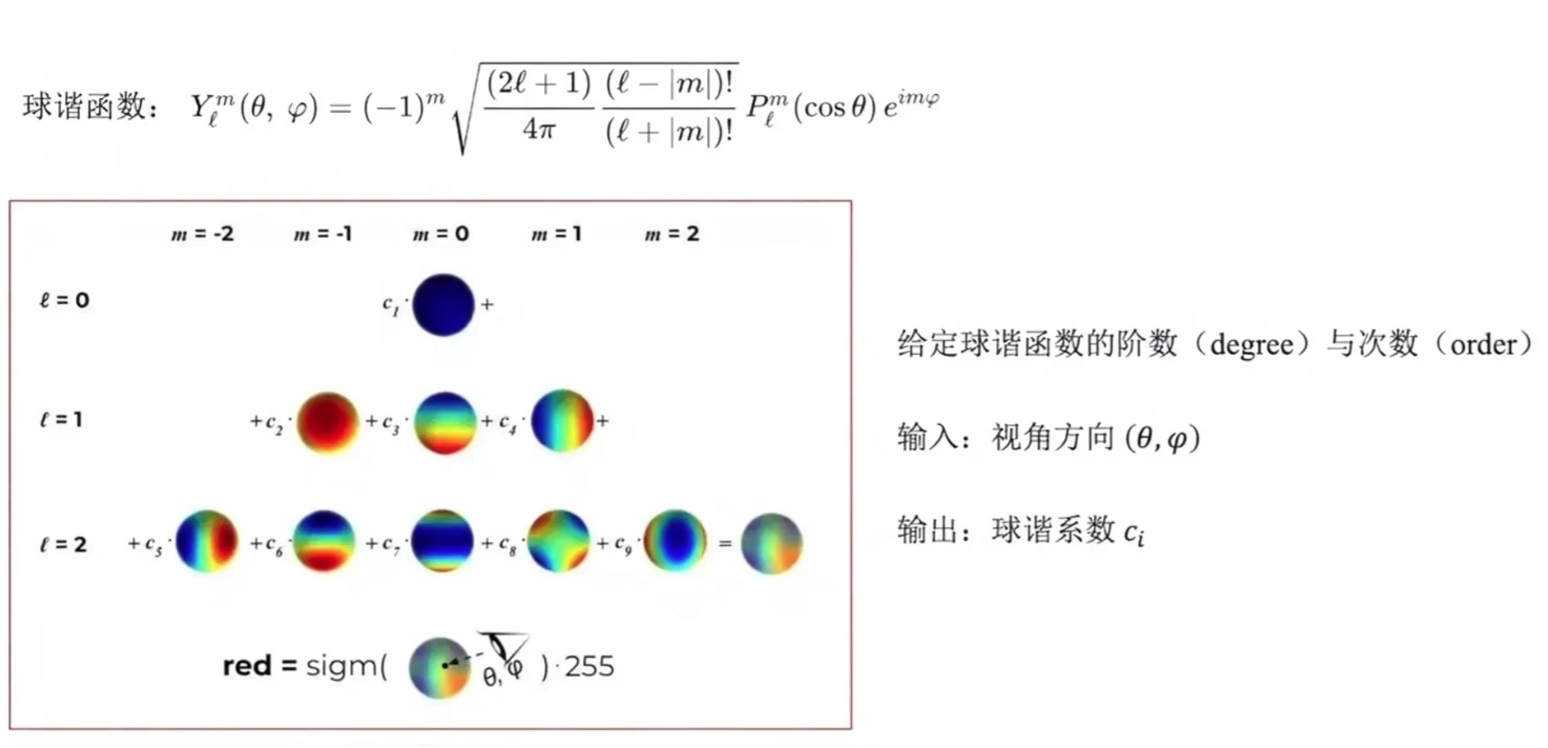
sh 不直接使用RGB的原因：颜色固定，无法很好的处理同一个物体在不同视角下的高光、反射。我们的期望是更好的处理RGB不能解决的问题

α-blending

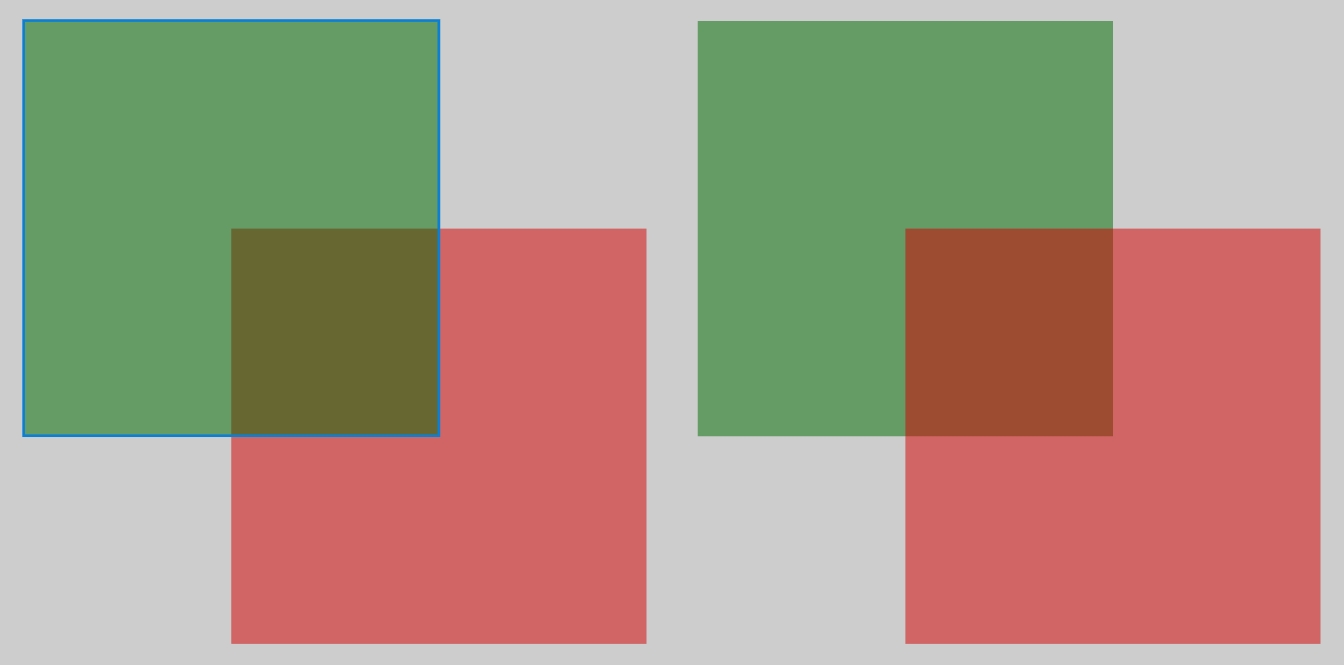
投影后的2D高斯通过Splatting绘制到图像。对于每个像素，需要混合所有覆盖它的高斯。

像素颜色计算

按深度从前到后排序N个高斯，像素颜色通过Alpha混合累积（论文公式3）：

C=∑i∈Nciαi∏j=1i−1(1−αj)C = \sum_{i \in N} c_i \alpha_i \prod_{j=1}^{i-1}(1 - \alpha_j)

其中：

  • cic_i：第i个高斯的颜色（从球谐函数SH计算，视角相关）
  • αi\alpha_i：第i个高斯在该像素的有效不透明度
αi=oi⋅exp⁡(−12(x−μi′)T(Σi′)−1(x−μi′))\alpha_i = o_i \cdot \exp\left(-\frac{1}{2}(\mathbf{x} - \mu_i')^T (\Sigma_i')^{-1} (\mathbf{x} - \mu_i')\right)

其中 oi∈[0,1]o_i \in [0,1] 是可学习的不透明度参数，指数项为2D高斯函数（中心为1，边缘趋于0）

  • Ti=∏j=1i−1(1−αj)T_i = \prod_{j=1}^{i-1}(1 - \alpha_j)：透射率，表示前面所有高斯的累积透光率

物理意义：

  • 前景高斯会遮挡后面的高斯
  • 半透明高斯允许后面的颜色透过
  • 类似传统图形学的Alpha混合

Early Stopping

当透射率接近0时（几乎完全被遮挡），后续高斯的贡献可忽略：

Ti=∏j=1i−1(1−αj)<ϵT_i = \prod_{j=1}^{i-1}(1 - \alpha_j) < \epsilon

通常设置 ϵ=0.001\epsilon = 0.001，提前终止可大幅加速渲染（跳过被完全遮挡的高斯）。

Splatting2

优化过程

损失函数

3DGS使用组合损失函数，平衡像素精度和感知质量：

L=(1−λ)L1+λLD-SSIM\mathcal{L} = (1-\lambda)\mathcal{L}_1 + \lambda \mathcal{L}_{\text{D-SSIM}}

其中 λ=0.2\lambda = 0.2 是权重系数，控制两种损失的相对重要性。

L1 损失（像素级精度）
L1=1HW∑x,y∣Irender(x,y)−IGT(x,y)∣\mathcal{L}_1 = \frac{1}{HW}\sum_{x,y} |I_{\text{render}}(x,y) - I_{\text{GT}}(x,y)|
  • 计算渲染图像与真实图像每个像素的绝对误差
  • 直接优化颜色准确性
  • 对离群值鲁棒（相比L2）
D-SSIM 损失（结构相似性）

SSIM（Structural Similarity Index） 是图像质量评价指标，模拟人眼感知（亮度，对比度，纹理结构）：

SSIM(x,y)=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)\text{SSIM}(x,y) = \frac{(2\mu_x\mu_y + C_1)(2\sigma_{xy} + C_2)}{(\mu_x^2 + \mu_y^2 + C_1)(\sigma_x^2 + \sigma_y^2 + C_2)}

其中：

  • μx,μy\mu_x, \mu_y：图像块的平均亮度（对比亮度）
  • σx2,σy2\sigma_x^2, \sigma_y^2：方差（对比对比度）
  • σxy\sigma_{xy}：协方差（对比结构相关性）
  • C1,C2C_1, C_2：稳定常数（避免除零）

D-SSIM（用于损失函数）：

LD-SSIM=1−SSIM2\mathcal{L}_{\text{D-SSIM}} = \frac{1-\text{SSIM}}{2}

将相似性指标转换为损失（SSIM越大越好 → D-SSIM越小越好）

计算过程：

  1. 在图像上滑动窗口（通常11×11像素）
  2. 对每个窗口计算局部SSIM值
  3. 所有窗口的SSIM求平均
  4. 转换为损失值

SSIM关注三个维度：

  • 亮度：整体明暗是否一致
  • 对比度：局部明暗变化是否相似
  • 结构：纹理模式是否匹配
为什么组合使用？
损失类型优点缺点权重
L1像素精度高，收敛快可能过度平滑，忽略结构80%
D-SSIM保持边缘锐利，纹理清晰计算复杂，可能颜色漂移20%

组合效果：

  • L1主导优化方向（稳定训练）
  • D-SSIM辅助优化细节（提升主观质量）
  • 达到客观精度和感知质量的平衡

反向传播梯度

不依赖PyTorch的自动计算，而是手动推导加速计算

由于渲染过程完全可微：

∂L∂θ←反向传播\frac{\partial \mathcal{L}}{\partial \theta} \leftarrow \text{反向传播}

可直接优化所有参数：

  • 3D位置 μ
  • 旋转 q
  • 缩放 s
  • 不透明度 α
  • SH系数 k

使用Adam优化器，学习率随训练动态调整。

自适应密度控制

密度控制

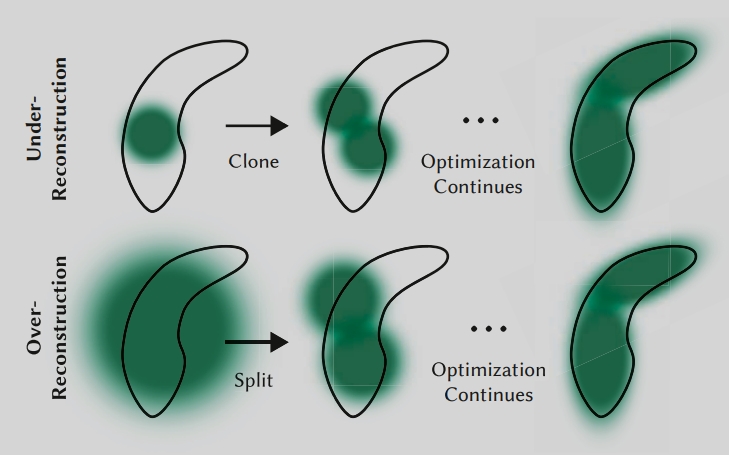
  1. 删除：定期删除几乎透明的高斯
  2. 克隆：对重建不足的高斯点进行克隆
  3. 分裂：对过度重建的高斯点进行分裂
  4. 定期重置不透明度：防止过渡增长
  5. 关键参数：分裂缩放因子 φ=1.6φ=1.6(经验得到)，不透明度阈值εα=0.005ε_α = 0.005

快速瓦片渲染

传统Splatting逐高斯渲染效率低，3DGS采用Tile-based Rasterization加速。

示意图 tile

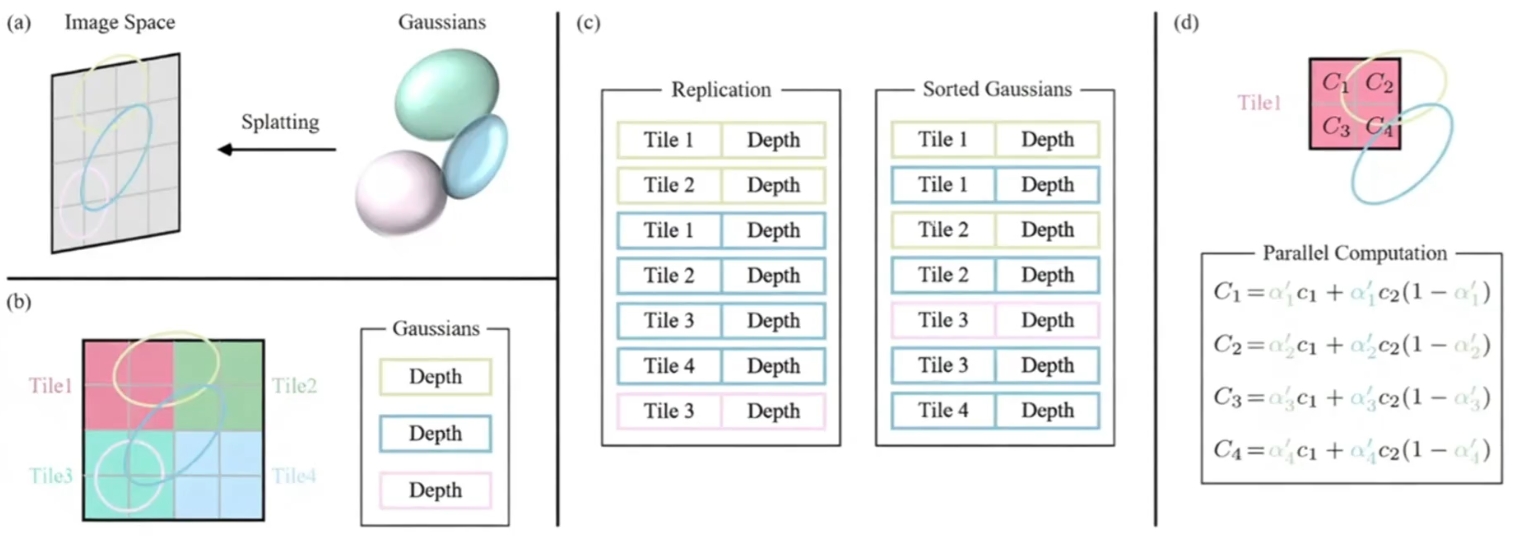
核心思想 

1
2
3

for 每个高斯:
  for 覆盖的像素:
    累积颜色
1
2
3

1. 图像分块（16×16 tiles）
2. 预处理：每个高斯分配到相关tile
3. 每个tile独立并行渲染

渲染流程

  1. 投影与剔除：

    • 将3D高斯投影到2D
    • 剔除视锥外的高斯

  2. Tile分配：

    • 计算每个2D高斯的包围盒
    • 将高斯ID加入覆盖的tile列表

  3. 排序：

    • 每个tile内按深度排序高斯（利用GPU排序）

  4. 并行渲染：

    • 每个tile启动一个线程块
    • 独立执行Alpha混合
更新于 2025-12-03 
返回 | 主页

目录