KamiertopのBlogSite
KamiertopのBlogSite

A Hierarchical 3D Gaussian Representation for Real Time Rendering of Very Large Datasets

用于实时渲染超大型数据集的分层 3D 高斯表示

kamiertop kamiertop 收录于 Paper
 约 6300 字 预计阅读 13 分钟 
/paper/h3dgs/cover_h3dgs.png
Paper_Project https://repo-sam.inria.fr/fungraph/hierarchical-3d-gaussians/ card image

3D重建

3DGS开山作 https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/ card image

3D重建是什么

从 2D 图像、视频、点云等输入数据中，还原真实场景或物体的 3D 几何结构、外观信息（颜色、纹理、光照），最终生成可交互、可渲染的3D数字化模型的过程

diff

应用场景在哪里

  • 消费娱乐：AR/VR，影视游戏
  • 工业
  • 文化遗产保护
  • 医疗健康
  • 自动驾驶

为什么使用3DGS

  • 3D降维后依然是高斯，仿射变换之后依然是高斯
  • 之前使用NERF，使用神经网络表示
  • 基于体素的显式场景表示，可直接投影到2D进行快速光栅化，支持实时渲染
  • 可微分（支持梯度下降优化），渲染质量高

不同建模方式对比

基于3DGS的其他工作

Feature-3DGS https://feature-3dgs.github.io/ card image DreamScene360 https://dreamscene360.github.io/ card image

概述

  • 无深度学习?
  • 简单的机器学习
  • 大量的CG知识
  • 复杂的线性代数
  • 高性能GPU编程

前置基础

高斯分布

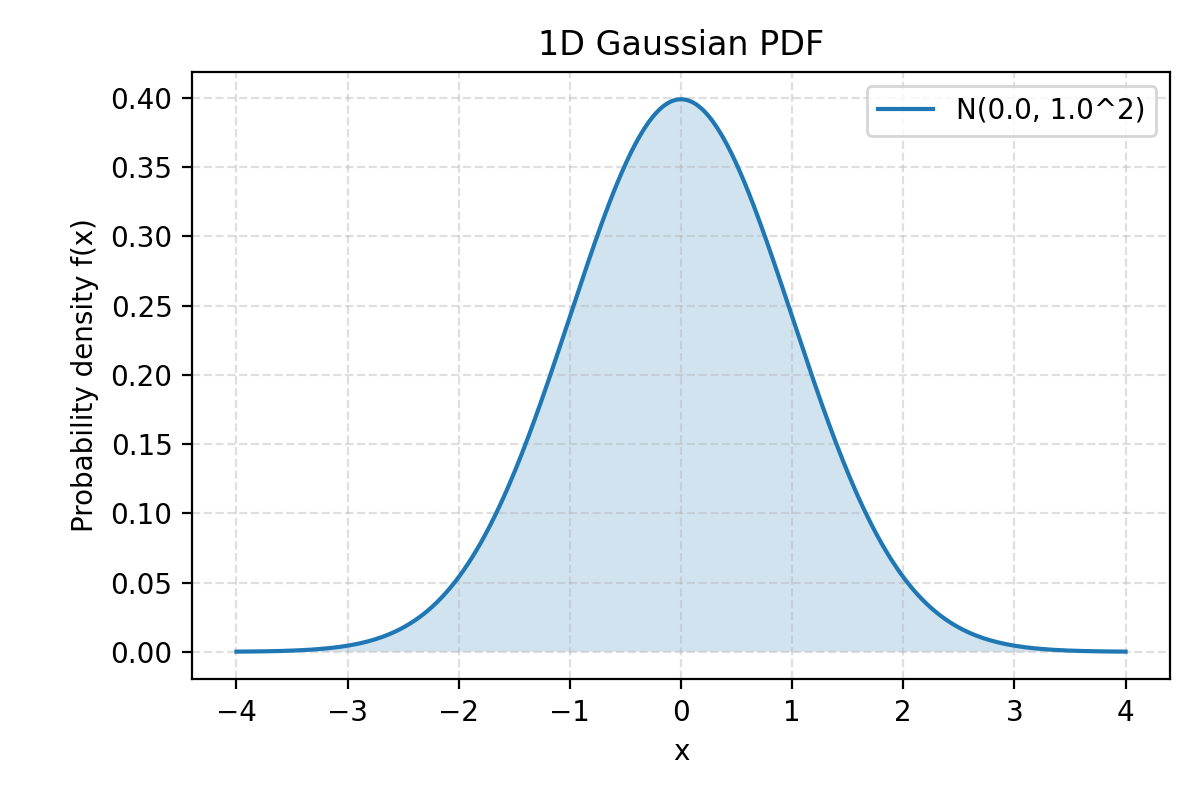
一维高斯函数

通常用于表示一维数据（如时间序列或数值）的概率分布

f(x;μ,σ2)=12πσ2e−(x−μ)22σ2f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
符号含义
f(x)f(x)函数在 xx 处的取值（概率密度）
xx随机变量（自变量）
μ\mu均值 (Mean)：曲线的中心位置
σ2\sigma^2方差 (Variance)：数据的分散程度
σ\sigma标准差 (Standard Deviation)：方差的平方根

1dgs

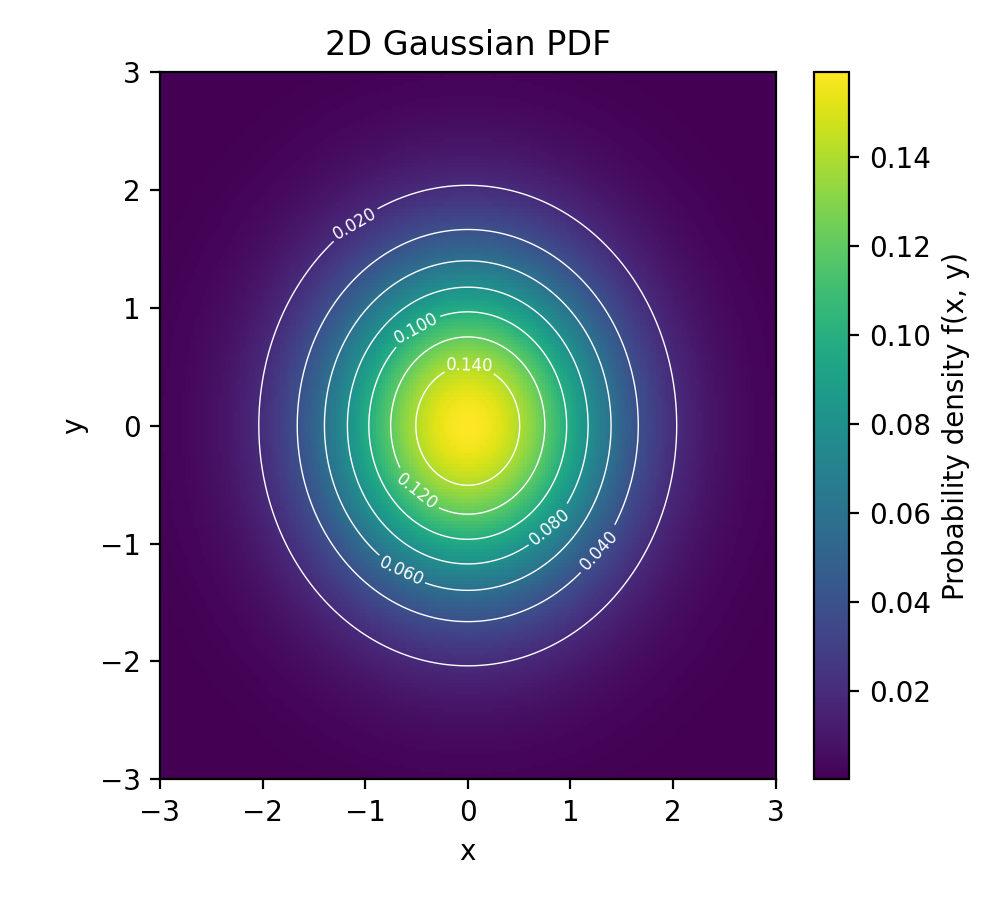
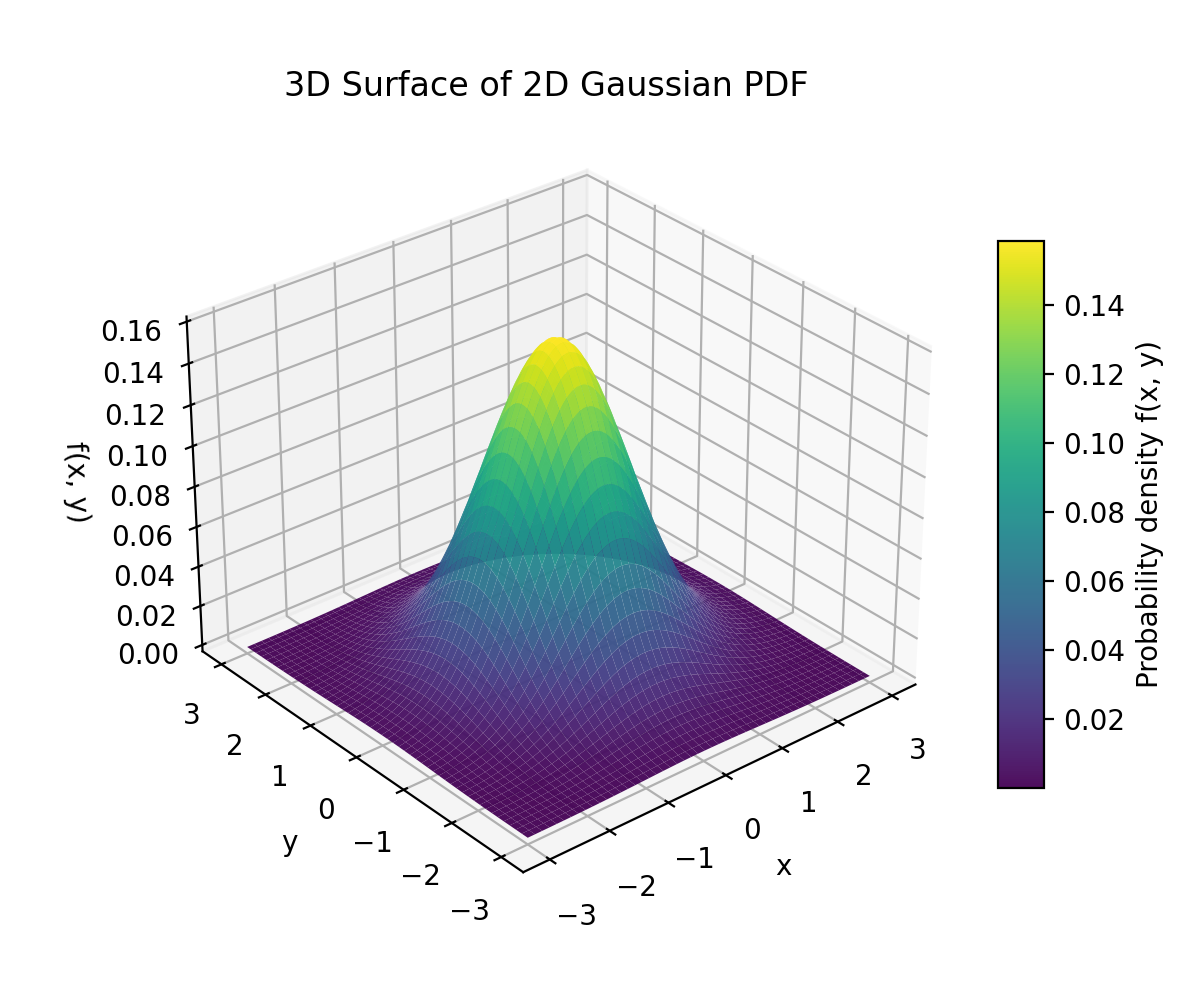
二维高斯函数

通常用于图像处理和表示二维平面上的概率分布。它使用一个均值向量 μ\boldsymbol{\mu} 和一个协方差矩阵 Σ\boldsymbol{\Sigma}

f(x;μ,Σ)=12πdet⁡(Σ)e−12(x−μ)TΣ−1(x−μ)f(\mathbf{x}; \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{2\pi \sqrt{\det(\boldsymbol{\Sigma})}} e^{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x}-\boldsymbol{\mu})}
符号含义
x\mathbf{x}二维向量 (xy)\begin{pmatrix} x \\ y \end{pmatrix}
μ\boldsymbol{\mu}均值向量 (μxμy)\begin{pmatrix} \mu_x \\ \mu_y \end{pmatrix}：分布的中心位置
Σ\boldsymbol{\Sigma}协方差矩阵 (Covariance Matrix)：一个 2×22 \times 2 矩阵，描述 xx 和 yy 的方差和它们之间的协方差
det⁡(Σ)\det(\boldsymbol{\Sigma})协方差矩阵的行列式

2dgs 2dgs

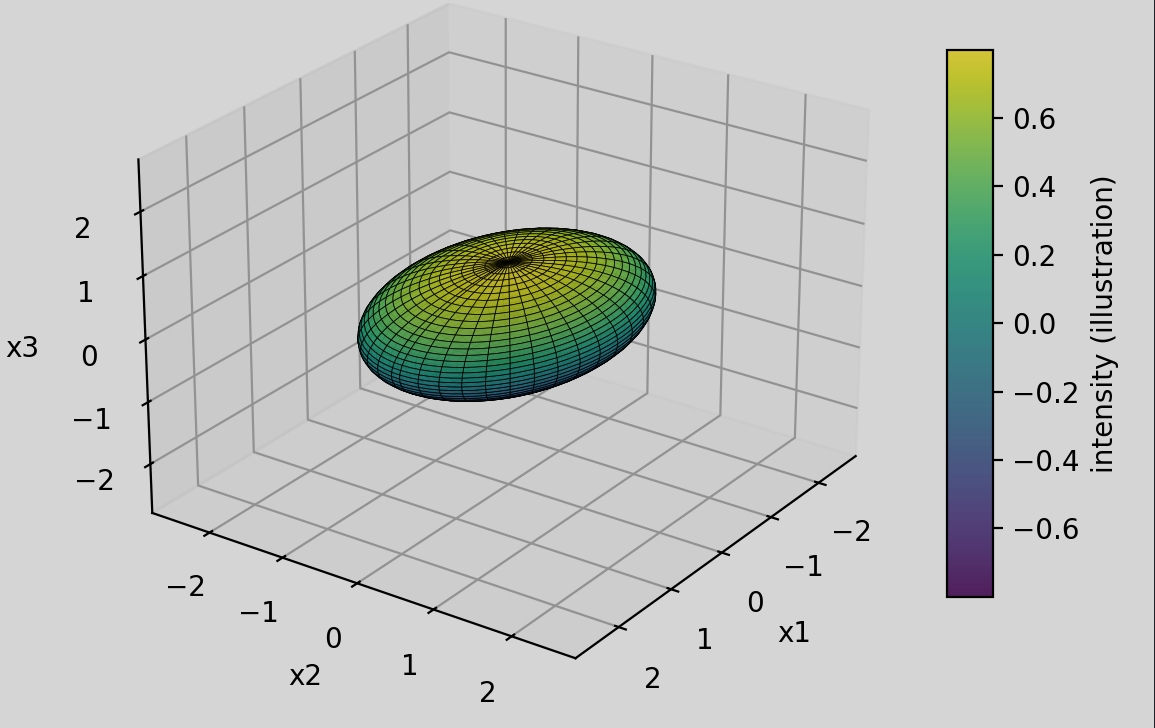
三维高斯函数

通常用于表示三维空间中的概率分布, 例如在3DGS中描述一个椭球

f(x;μ,Σ)=1(2π)3det⁡(Σ)e−12(x−μ)TΣ−1(x−μ)f(\mathbf{x}; \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{\sqrt{(2\pi)^3 \det(\boldsymbol{\Sigma})}} e^{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x}-\boldsymbol{\mu})}
符号含义
x\mathbf{x}三维向量 (xyz)\begin{pmatrix} x \\ y \\ z \end{pmatrix}：空间中的一个点
μ\boldsymbol{\mu}均值向量 (μxμyμz)\begin{pmatrix} \mu_x \\ \mu_y \\ \mu_z \end{pmatrix}：椭球的中心点（位置）
Σ\boldsymbol{\Sigma}协方差矩阵 (Covariance Matrix)：一个 3×33 \times 3 矩阵，它完全定义了椭球体的形状、大小和旋转方向。在 3DGS 中，这个矩阵就是用来定义椭球几何的关键参数

3dgs

协方差矩阵

方差

方差描述单个随机变量 XX 相对于其均值 μX\mu_X 的离散程度

Var(X)=E[(X−μX)2]\text{Var}(X) = E[(X - \mu_X)^2]

协方差

协方差描述两个随机变量 XX 和 YY 之间的线性关系方向（同向变化还是反向变化）

Cov(X,Y)=E[(X−μX)(Y−μY)]\text{Cov}(X, Y) = E[(X - \mu_X)(Y - \mu_Y)]
  • Cov(X,Y)>0\text{Cov}(X, Y) > 0: XX 和 YY 倾向于同向变化。
  • Cov(X,Y)<0\text{Cov}(X, Y) < 0: XX 和 YY 倾向于反向变化。
  • Cov(X,Y)=0\text{Cov}(X, Y) = 0: XX 和 YY 线性不相关。

二维协方差矩阵

Σ=(Cov(X,X)Cov(X,Y)Cov(Y,X)Cov(Y,Y)) \boldsymbol{\Sigma} = \begin{pmatrix} \text{Cov}(X, X) & \text{Cov}(X, Y) \\ \text{Cov}(Y, X) & \text{Cov}(Y, Y) \end{pmatrix}

三维协方差矩阵

Σ=(Var(X)Cov(X,Y)Cov(X,Z)Cov(X,Y)Var(Y)Cov(Y,Z)Cov(X,Z)Cov(Y,Z)Var(Z)) \boldsymbol{\Sigma} = \begin{pmatrix} \text{Var}(X) & \text{Cov}(X, Y) & \text{Cov}(X, Z) \\ \text{Cov}(X, Y) & \text{Var}(Y) & \text{Cov}(Y, Z) \\ \text{Cov}(X, Z) & \text{Cov}(Y, Z) & \text{Var}(Z) \end{pmatrix}
Σ=(σX2σXYσXZσXYσY2σYZσXZσYZσZ2) \boldsymbol{\Sigma} = \begin{pmatrix} \sigma_X^2 & \sigma_{XY} & \sigma_{XZ} \\ \sigma_{XY} & \sigma_Y^2 & \sigma_{YZ} \\ \sigma_{XZ} & \sigma_{YZ} & \sigma_Z^2 \end{pmatrix}

举例说明

X=(1,2,3,4,5)X = (1, 2, 3, 4, 5), Y=(1,3,3,5,8)Y = (1, 3, 3, 5, 8)

μX=3\mu_X = 3, μY=4\mu_Y = 4

XiΔX=Xi−3YiΔY=Yi−4ΔX⋅ΔY
1-21-36
2-13-11
303-10
41511
52848
∑\sum∑(ΔX)2=10\sum (\Delta X)^2 = 10∑(ΔY)2=28\sum (\Delta Y)^2 = 28∑(ΔX)(ΔY)\sum (\Delta X)(\Delta Y)=16

Var(X)=∑(Xi−μX)2N=105=2\text{Var}(X) = \frac{\sum (X_i - \mu_X)^2}{N} = \frac{10}{5} = 2

Var(Y)=∑(Yi−μY)2N=285=5.6\text{Var}(Y) = \frac{\sum (Y_i - \mu_Y)^2}{N} = \frac{28}{5} = 5.6

XX 和 YY 的协方差 (Cov(X,Y)\text{Cov}(X, Y)): Cov(X,Y)=∑(Xi−μX)(Yi−μY)N=165=3.2\text{Cov}(X, Y) = \frac{\sum (X_i - \mu_X)(Y_i - \mu_Y)}{N} = \frac{16}{5} = 3.2

协方差矩阵：

Σ=(2.03.23.25.6) \boldsymbol{\Sigma} = \begin{pmatrix} 2.0 & 3.2 \\ 3.2 & 5.6 \end{pmatrix}

论文讲解

背景

如何基于3DGS做场景重建

光栅化器是把 “几何图元（比如点、线、面、3D 高斯）” 转换成 “屏幕像素” 的工具

重建流程

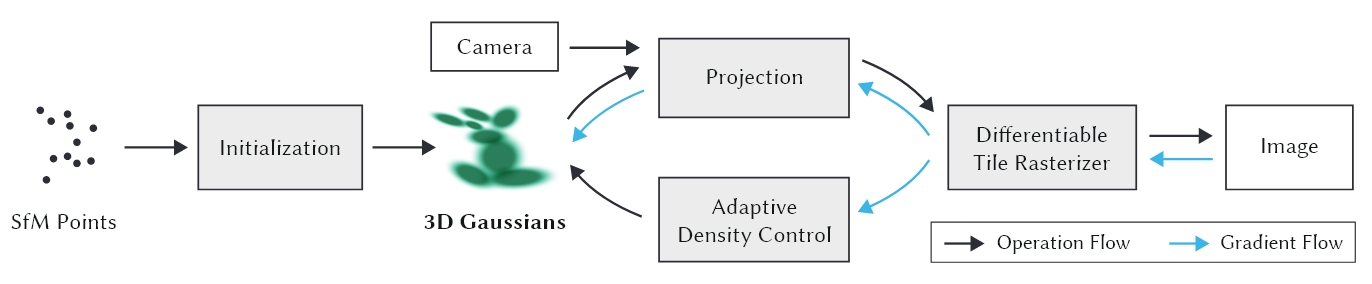
高斯基元参数

  • 均值：μμ
  • 协方差矩阵：∑\sum
  • 不透明度: oo
  • 球谐函数: SHSH
  • α-blending权重: G(x,y)=e−12([x,y]T−μ′)T∑′−1([x,y]T−μ′)G(x, y)=e^{-\frac{1}{2}\left([x, y]^{T}-\mu'\right)^{T} \sum^{\prime-1}\left([x, y]^T-\mu'\right)}

马氏距离衡量一个样本到一组数据或某个中心的真实相似程度

D2=([x,y]T−μ′)T∑′−1([x,y]T−μ′)D^2 = {\left([x, y]^T-\mu'\right)^T \sum^{\prime-1}\left([x, y]^{T}-\mu'\right)} ，其中μ′=[x,y]T\mu'=[x,y]^T

研究动机与目标

  • 现有的3D高斯渲染方法（如3D Gaussian Splatting）虽然在视觉质量和实时渲染方面表现出色，但受限于资源（如内存和计算能力），无法处理大规模场景
  • 论文提出了一种分而治之的策略，通过将场景划分为多个“块”（chunks），并为每个块构建独立的层次化3D高斯表示，从而实现大规模场景的高效训练和实时渲染

核心

分层LOD

  1. 构建一个基于3D高斯的层次化树结构，每个节点都是一个3D高斯体元，能够高效表达场景的细节和概要

  2. 通过选择不同层次的节点进行渲染，实现了根据视点距离自动调整细节层次的功能，减轻渲染压力

横看成岭侧成峰，远近高低各不同

LOD 现实体验是距离远看的小，距离近看的大，所以我们希望远处物体使用大的粗粒度的3DGS去渲染，减少同时渲染的个数；对于近处的物体渲染更多细节，保证视觉质量

首先对所有的3DGS进行分层构建出一个层次结构，这里使用包围盒（BVH）来做，最后物理上相近的，更可能表示同一个物体的高斯球被分在一起 bvh1 (上下两张图片均来源于B站UP主：来点盐巴吧) bvh1

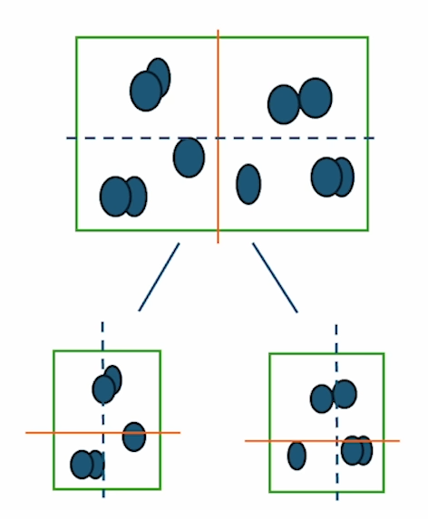
现在相近的都被分在了一起，开始构建粗粒度高斯，所有细粒度的高斯作为最下层，从下至上构建新的高斯

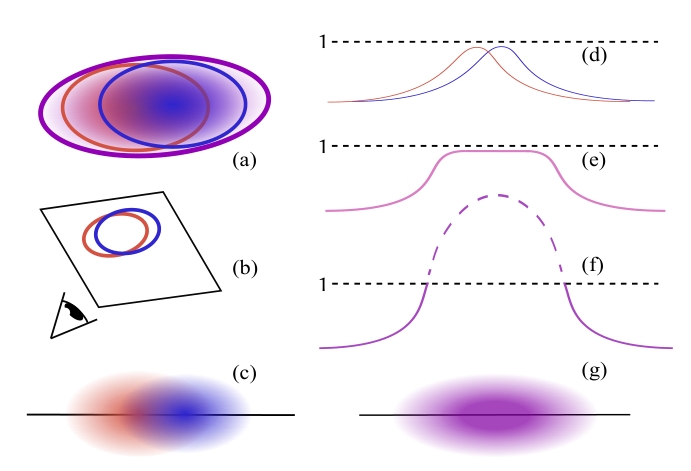
中间节点生成

中间节点也是高斯，也具有上述属性/参数，需要推理这些节点的值

这些节点通过两两合并生成，新高斯球的属性由两个子高斯的属性加权生成（从下至上，叶子节点也就是最细粒度的是第l层，新生成的是l+1层）

合并后均值：μ(l+1)=∑iNwiμi(l)\boldsymbol{\mu}^{(l+1)}=\sum_{i}^{N}w_{i}\boldsymbol{\mu}_{i}^{(l)}

合并后的协方差矩阵：Σ(l+1)=∑iNwi(Σi(l)+(μi(l)−μ(l+1))(μi(l)−μ(l+1))T)\boldsymbol{\Sigma}^{(l+1)}=\sum_{i}^{N}w_{i}(\boldsymbol{\Sigma}_{i}^{(l)}+(\boldsymbol{\mu}_{i}^{(l)}-\boldsymbol{\mu}^{(l+1)})(\boldsymbol{\mu}_{i}^{(l)}-\boldsymbol{\mu}^{(l+1)})^{T})

归一化权重wi=wi′∑iNwi′w_i=\frac{w_i^{\prime}}{\sum_i^{N} w_i^{\prime}}

单个高斯对像素的颜色贡献：Ci(x,y)=oiciG(x,y)C_{i}(x, y)= o_i c_i G(x, y) (cic_i是高斯颜色)

高斯对整个图像的总贡献 CiC_i：Ci=oici∫X∫YG(x,y)=oici(2π)2∣Σ′∣C_i = o_i c_i \int_X \int_Y G(x,y) = o_i c_i \sqrt{(2\pi)^{2}|\Sigma^{\prime}|} 考虑简单情况，我们希望父节点和子节点高斯分布贡献度相同：gpg_p = g1g_1 + g2g_2

所以需要父节点的CpC_p = C1+C2C_1+C_2，忽略与权重无关的常数因子和颜色： wi′=oici(2π)2∣Σ′∣w_i^{\prime} = o_i c_i \sqrt{(2\pi)^{2}|\Sigma^{\prime}|}

在实际应用中，由于高斯分布的二维协方差矩阵的行列式的平方根与对应三维椭球体的（投影）表面积成正比，我们计算每个椭球体的表面积SiS_i

合并后的SH：SH(l+1)=SH1(l)w1+SH2(l)w2SH^{(l+1)}=SH_{1}^{(l)}w_{1}+SH_{2}^{(l)}w_{2}

不透明度需要特殊处理：∑iNwi′Sp\frac{\sum_{i}^{N}w_{i}^{\prime}}{S_p}

不透明度

层次选择

给定一个视角，我们需要找到一个层次去渲染

层次选择

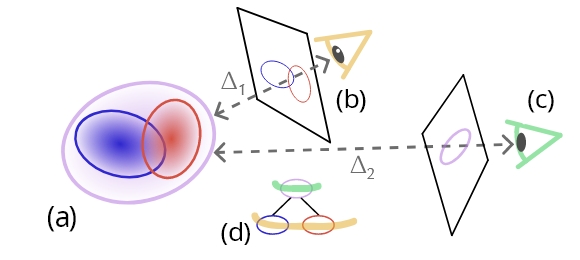
  1. 定义粒度，量化层次节点的屏幕投影大小
  2. 设定目标粒度阈值，划定当前视角的细节需求，阈值的本质是 “用像素尺寸定义‘可接受的细节模糊度’”—— 当节点投影粒度≤阈值时，人眼难以察觉细节损失，此时用该节点渲染可兼顾效率；若粒度超过阈值，会出现明显的 “块状模糊”，需切换到更细的子节点
  3. 层次切割，筛选满足阈值的最深节点

层次选择

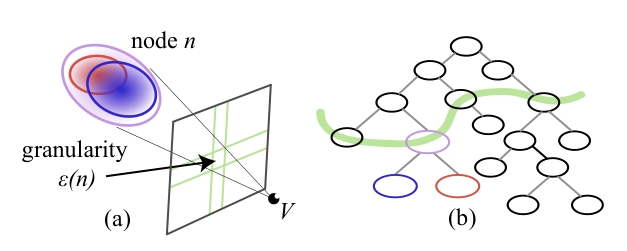
层次过渡与插值

为了保证视觉质量，可以通过插值父节点和子节点的高斯属性来实现，使得层次之间过渡平滑

由层次选择返回的切分将包含满足过渡标准的节点，通过评估切分中每个节点的粒度以及其父节点pp的粒度， 选择插值权重。

Attr=TnAttrp+(1−Tn)AttrcAttr = T_n Attr_p + (1-T_n) Attr_c

权重公式，τϵ\tau_{\epsilon}是目标粒度，ϵ(n)\epsilon(n)表示子节点粒度

tn=τϵ−ϵ(n)ϵ(p)−ϵ(n)(10)t_{n} = \frac{\tau_{\epsilon} - \epsilon(n)}{\epsilon(p) - \epsilon(n)} \quad (10)

位置，颜色和球谐系数可以使用插值权重进行插值，对于协方差矩阵，执行方向匹配

节点优化与层次压缩

FastGS https://fastgs.github.io/ card image
  1. 标记所有的叶子节点，通过粒度选择满足阈值的节点，移除其他节点
  2. 优化节点属性，确保不同层级节点都能匹配全分辨率下的视觉细节

分块训练与优化

为了加速训练，首先训练一个大的脚手架，随后对场景分块，支持并行训练，最后合并为一个大的场景

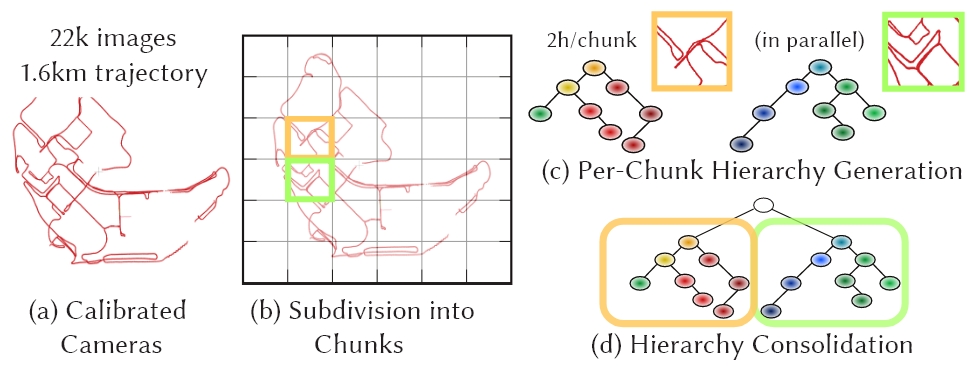
chunk

环境搭建和代码复现

环境
  • OS：Ubuntu 22.04.5 LTS
  • GPU：NVIDIA GeForce RTX 4070 12GB
  • Memory：64GB
  • CPU: AMD Ryzen 7 7900X

(建议使用ubuntu-22.04)

安装 GCC/G++

直接使用apt安装 sudo apt install -y gcc-10 g++-11

版本验证 gcc-11 -v g++-11 -v

符号链接

1
2
3
4

sudo ln -s /usr/bin/gcc-11 /usr/bin/gcc
sudo ln -s /usr/bin/g++-11 /usr/bin/g++
gcc -v
g++ -v

下载CUDA Toolkit

这里使用12.1

cuda-toolkit-archive https://developer.nvidia.com/cuda-toolkit-archive card image

可以在上面的归档页面中选择版本以及适合的操作系统和发行版

1
2
3
4

sudo apt install wget -y
wget https://developer.download.nvidia.com/compute/cuda/12.1.0/local_installers/cuda_12.1.0_530.30.02_linux.run

sudo sh cuda_12.1.0_530.30.02_linux.run

稍后会弹出一个窗口，输入accept，后面再选择Install即可

设置PATH和LD_LIBRARY_PATH

1
2
3
4

# 如果用的是bash，需要输出到：.bashrc
echo 'export PATH=/usr/local/cuda-12.1/bin:$PATH' >> ~/.zshrc
echo 'export LD_LIBRARY_PATH=/usr/local/cuda-12.1/lib64:$LD_LIBRARY_PATH' >> ~/.zshrc
source ~/.zshrc

检查nvcc版本：nvcc --version，输出大致如下

1
2
3
4

Copyright (c) 2005-2023 NVIDIA Corporation
Built on Tue_Feb__7_19:32:13_PST_2023
Cuda compilation tools, release 12.1, V12.1.66
Build cuda_12.1.r12.1/compiler.32415258_0

编译colmap

显卡计算能力

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

sudo apt update
sudo apt install -y \
    git \
    cmake \
    ninja-build \
    build-essential \
    libboost-program-options-dev \
    libboost-graph-dev \
    libboost-system-dev \
    libeigen3-dev \
    libfreeimage-dev \
    libmetis-dev \
    libgoogle-glog-dev \
    libgtest-dev \
    libgmock-dev \
    libsqlite3-dev \
    libglew-dev \
    qtbase5-dev \
    libqt5opengl5-dev \
    libcgal-dev \
    libceres-dev \
    libcurl4-openssl-dev \
    libmkl-full-dev

编译colmap, 由于需要cuda支持, 所以增加参数: -DCMAKE_CUDA_ARCHITECTURES=native -DCMAKE_CUDA_ARCHITECTURES=89, DCMAKE_CUDA_ARCHITECTURES需要根据自己的显卡来设置

1
2
3
4
5
6

git clone https://github.com/colmap/colmap.git
cd colmap
mkdir build &&  cd build
cmake .. -GNinja -DBLA_VENDOR=Intel10_64lp -DCMAKE_CUDA_ARCHITECTURES=native -DCMAKE_CUDA_ARCHITECTURES=89
ninja
sudo ninja install

最后检查是否成功

1
2
3

which colmap

colmap -h

配置项目环境

需要使用conda, 请提前配置好conda, 我这里使用的是miniforge

配置虚拟环境 

1
2
3
4
5
6
7

cd ~
git clone https://github.com/graphdeco-inria/hierarchical-3d-gaussians.git --recursive
cd hierarchical-3d-gaussians
conda create -n hierarchical_3d_gaussians python=3.12 -y
conda activate hierarchical_3d_gaussians
pip install torch==2.3.0 torchvision==0.18.0 torchaudio==2.3.0 --index-url https://download.pytorch.org/whl/cu121
pip install -r requirements.txt

下载权重 

1
2

wget -P submodules/Depth-Anything-v2/checkpoints https://huggingface.co/depth-anything/Depth-Anything-V2-Large/resolve/main/depth_anything_v2_vitl.pth
wget -P submodules/DPT/weights/ https://github.com/intel-isl/DPT/releases/download/1_0/dpt_large-midas-2f21e586.pt

编译层次结构生成器与合并器 

1
2
3
4

cd submodules/gaussianhierarchy
cmake . -B build -DCMAKE_BUILD_TYPE=Release
cmake --build build -j --config Release
cd ../..

编译实时查看器

我实验时发现不能一次下载所有的, AI提示分步下载

1
2
3

sudo apt install -y cmake libglew-dev libassimp-dev libboost-all-dev libgtk-3-dev libopencv-dev libglfw3-dev

sudo apt install -y libavdevice-dev libavcodec-dev libeigen3-dev libxxf86vm-dev libembree-dev

克隆层次查看器并构建

速度可能会很慢, 耐心等待

1
2
3
4

cd SIBR_viewers
git clone https://github.com/graphdeco-inria/hierarchy-viewer.git src/projects/hierarchyviewer
cmake . -B build -DCMAKE_BUILD_TYPE=Release -DBUILD_IBR_HIERARCHYVIEWER=ON -DBUILD_IBR_ULR=OFF -DBUILD_IBR_DATASET_TOOLS=OFF -DBUILD_IBR_GAUSSIANVIEWER=OFF
cmake --build build -j --target install --config Release

运行

到这里环境就已经配置完成了, 接下来按照官方文档一步一步执行就可以了

初步运行结果(待更新)

  • 官方小数据，大约1500张图片，421MB：训练需要176min
  • 自己数据集，500张图片,3.5GB: 训练需要134min

代码流程

  1. 准备数据集，配置环境变量：DATASET_DIR (建议使用绝对路径)
  2. 预处理阶段
    1. 生成全局 COLMAP （相机标定+稀疏点云）
    2. 将全局COLMAP切成多个 chunk
    3. 生成单目深度图+深度标定参数（可选但建议）
  3. 优化阶段，有两种方法
    1. 一键端到端脚本：python scripts/full_train.py --project_dir ${DATASET_DIR}
    2. 手动优化（基本上就是论文中的流程）
      1. Coarse优化：训练全局脚手架（scaffold）
      2. 单个chunk的首次训练（独立3DGS）
      3. 为每个chunk构建层次结构
      4. 单个chunk的层次结构后优化
      5. 所有chunk的层次结构合并
更新于 2025-11-02 
返回 | 主页

目录