FastGS: Training 3D Gaussian Splatting in 100 Seconds

Project_Page fastgs.github.io/

背景

• 3DGS的自适应密度控制机制存在缺陷, 产生大量冗余高斯体, 增加训练时间和渲染开销
• 对多视图一致性的利用不足
• 渲染管线存在冗余开销

核心

Multi-View Consistent Densification(VCD)

传统的3DGS通过低透明度或规模过大移除冗余, 不能高效解决冗余高斯的问题

1. 从全部训练视图中随机选取K个视图(10)$V=\{v^j\}_{j=1}^K$, 以及真实图像$G=\{g^j\}_{j=1}^K$和渲染之后的图像$R=\{r^j\}_{j=1}^K$

2. 对于每一个视角$v^j$, 计算渲染图$r^{j}_{u,v}$和真实图$g^{j}_{u,v}$在像素$(u,v)$的误差:

   $$e_{u,v}^{j}=\frac{1}{C^{\prime}}\sum_{c^{\prime}=1}^{C^{\prime}}{\left| r_{u,v}^{j,c^{\prime}}-g_{u,v}^{j,c^{\prime}} \right|}$$

   这里的$c^{\prime} \in \{1,2,\dots,C^{\prime}\}$表示颜色的通道, 公式意思是计算通道的误差的平均值

3. 接下来构造该视图的损失图$\mathcal{M}^j\in \mathbb{R}^{W\times H}$

   $$\mathcal{M} ^j=\mathcal{N} \left( \{\,e_{u,v}^{j}\,\}_{u=0,v=0}^{W-1,H-1} \right)$$

   $W$表示width, $H$表示height, $\mathcal{N} (\cdot )$表示对结果进行最小-最大归一化

4. 设置阈值$\tau_d$筛选出高误差像素, 也就是渲染质量差的区域, 形成高误差掩码

   $$\mathcal{M}^j_\text{mask} = \mathbb{I}(\mathcal{M}^j > \tau)$$

5. 对于像素$P$来说, $\mathcal{M}^j_\text{mask}(u,v) = 1$表示渲染质量差

6. 

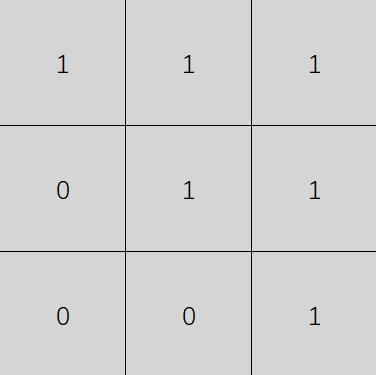
7. 接下来需要找到质量差的像素是由哪些高斯负责的

   1. 3DGS投影到2D图像平面, 可以得到在该视图下的2D覆盖范围(足迹)$\Omega_i$
   2. 统计每个高斯体的2D足迹包含的高误差像素数量, 对应该高斯体对应区域的渲染质量差

8. 对每个高斯体, 将其在K个视图中的高误差像素数量求和后取平均, 得到致密化重要性分数

   $$s_{d}^{i}=\frac{1}{K}\sum_{j=1}^K{\sum_p^{\varOmega _i}{\mathbb{I} \left( \mathcal{M} _{mask}^{j}\left( p \right) =1 \right)}}$$

9. 仅当重要性分数超过阈值$s^{i}_d$时, 才对其进行致密化, 确保新生成的高斯体聚焦于欠重建区域

Multi-View Consistent Pruning(VCP)

1. 针对每个视角 $v^j \in V$, 计算渲染图和真实图之间的损失, 这是因为要判断是否真正影响了 “多视角整体重建质量”, 不是只看覆盖了多少高误差像素

2. 引入初始论文中的整体视角误差:

   $$E_{\mathrm{photo}}^{j} = (1-\lambda) L_1^{j} + \lambda (1-L_{\mathrm{SSIM}}^{j})$$

3. 结合整体视角误差计算贡献度:

   $$s_p^{i}=\mathcal{N} \left( \sum_{j=1}^K{\left( \sum_p^{\varOmega _i}{\mathbb{I} \left( \mathcal{M} _{mask}^{j}\left( p \right) =1 \right)} \right) \cdot E_{\mathrm{photo}}^{j}} \right)$$

Compact Box